前置
主要参数
网络结构设计
% 网络结构: 3-6-2
% 输入层: 3节点(含偏置)
% 隐含层: 6节点,Sigmoid激活函数
% 输出层: 2节点,线性输出
w1 = rands(3, 6); % 输入层到隐含层权值
w2 = rands(6, 2); % 隐含层到输出层权值训练参数设置
xite = 0.50; % 学习率
alfa = 0.05; % 动量因子
max_epoch = 10000; % 最大迭代次数
error_goal = 1e-10; % 误差目标表格
1.BP神经网络训练样本
2.BP神经网络测试样本及结果
代码
% 清空工作区、关闭所有图形窗口、清空命令窗口
clear; % 清除工作区所有变量
close; % 关闭所有图形窗口
clc; % 清空命令窗口
%% 1. 样本生成和预处理
% 生成标准训练样本(3输入2输出,共3组样本)
x_train = [2, 0, 0; % 第一组输入样本:[2,0,0]
0, 1.5, 0; % 第二组输入样本:[0,1.5,0]
0, 0, 1]; % 第三组输入样本:[0,0,1]
y_train = [1, 0; % 第一组期望输出:[1,0]
0, 0.5; % 第二组期望输出:[0,0.5]
0, 1]; % 第三组期望输出:[0,2]
% 生成测试样本网格,用于逼近目标函数 Z = sin(x)·sin(y)
x_test = linspace(-pi, pi, 20); % 在[-π,π]区间生成20个等间距的x值
y_test = linspace(-pi, pi, 20); % 在[-π,π]区间生成20个等间距的y值
[X_test, Y_test] = meshgrid(x_test, y_test); % 生成测试网格点
Z_target = sin(X_test) .* sin(Y_test); % 计算目标函数值
% 将测试样本归一化到[0,1]范围,便于神经网络处理
X_test_norm = (X_test + pi) / (2*pi); % 将x从[-π,π]映射到[0,1]
Y_test_norm = (Y_test + pi) / (2*pi); % 将y从[-π,π]映射到[0,1]
%% 2. BP神经网络参数设置
xite = 0.50; % 学习率,控制权值更新步长
alfa = 0.05; % 动量因子,加速收敛并防止震荡
% 网络结构: 3-6-2 (输入层3节点,隐含层6节点,输出层2节点)
w2 = rands(6, 2); % 初始化隐含层到输出层的权值矩阵(6×2),随机值在[-1,1]之间
w2_1 = w2; % 保存上一时刻的权值,用于动量项计算
w2_2 = w2_1; % 保存上两个时刻的权值
w1 = rands(3, 6); % 初始化输入层到隐含层的权值矩阵(3×6)
w1_1 = w1; % 保存上一时刻的权值
w1_2 = w1; % 保存上两个时刻的权值
dw1 = zeros(size(w1)); % 初始化权值变化量矩阵
% 中间变量初始化
I = zeros(6, 1); % 隐含层神经元的输入值向量
Iout = zeros(6, 1); % 隐含层神经元的输出值向量(经过激活函数)
FI = zeros(6, 1); % 隐含层激活函数的导数值向量
OUT = 2; % 输出层节点数
k = 0; % 迭代次数计数器初始化
E = 1.0; % 误差初始值
NS = 3; % 训练样本数量
%% 3. 训练过程
max_epochs = 10000; % 最大迭代次数
E_threshold = 1e-20; % 误差阈值,当误差小于此值时停止训练
Ek = zeros(max_epochs, 1); % 预分配空间存储每次迭代的误差
times = 1:max_epochs; % 时间序列,用于绘图
% 显示训练开始信息
fprintf('开始BP神经网络训练...\n');
fprintf('网络结构: 3-6-2\n');
fprintf('学习率: %.2f, 动量因子: %.2f\n', xite, alfa);
% 主训练循环
while E >= E_threshold && k < max_epochs
k = k + 1; % 迭代次数加1
% 对每个样本进行训练(批量训练)
for s = 1:NS
x = x_train(s, :); % 获取第s个样本的输入
y = y_train(s, :); % 获取第s个样本的期望输出
% 前向传播过程
for j = 1:6 % 遍历隐含层每个神经元
I(j) = x * w1(:, j); % 计算隐含层第j个神经元的输入(加权和)
Iout(j) = 1/(1 + exp(-I(j))); % 使用S型激活函数计算输出
end
yl = w2' * Iout; % 计算输出层神经元的输入(加权和)
yl = yl'; % 转置为行向量
% 计算输出误差
el = y - yl; % 计算输出误差向量
sample_error = 0.5 * sum(el.^2); % 计算单个样本的均方误差
% 反向传播过程 - 权值调整
% 输出层到隐含层权值调整(使用梯度下降法)
w2 = w2_1 + xite * Iout * el + alfa * (w2_1 - w2_2);
% 隐含层到输入层权值调整
for j = 1:6
S = 1/(1 + exp(-I(j))); % 计算S型函数值
FI(j) = S * (1 - S); % 计算S型函数的导数
end
% 计算输入层到隐含层的权值调整量
for i = 1:3 % 遍历输入层每个节点
for j = 1:6 % 遍历隐含层每个节点
% 计算权值梯度(链式法则)
dw1(i,j) = xite * FI(j) * x(i) * (el(1)*w2(j,1) + el(2)*w2(j,2));
end
end
% 更新输入层到隐含层的权值
w1 = w1_1 + dw1 + alfa * (w1_1 - w1_2);
% 更新权值历史记录(用于动量项计算)
w1_2 = w1_1; % 保存上两个时刻的权值
w1_1 = w1; % 保存上一时刻的权值
w2_2 = w2_1; % 保存上两个时刻的权值
w2_1 = w2; % 保存上一时刻的权值
end
% 计算本轮所有样本的总误差
E = 0; % 重置误差
for s = 1:NS
x = x_train(s, :); % 获取样本输入
y = y_train(s, :); % 获取期望输出
% 前向传播计算实际输出
for j = 1:6
I(j) = x * w1(:, j); % 隐含层输入
Iout(j) = 1/(1 + exp(-I(j))); % 隐含层输出
end
yl = w2' * Iout; % 输出层输入
yl = yl'; % 转置
el = y - yl; % 计算误差
E = E + 0.5 * sum(el.^2); % 累加每个样本的误差
end
Ek(k) = E; % 记录本次迭代的误差
% 每1000次迭代显示一次进度
if mod(k, 1000) == 0
fprintf('迭代次数: %d, 误差: %.10f\n', k, E);
end
end
% 显示训练完成信息
fprintf('训练完成! 最终迭代次数: %d, 最终误差: %.10f\n', k, E);
%% 4. 绘制训练收敛过程
figure(1); % 创建图1
set(gcf, 'Position', [100, 400, 600, 400]); % 设置图形位置和大小
plot(times(1:k), Ek(1:k), '-.r', 'linewidth', 2); % 绘制误差曲线
xlabel('迭代次数 k'); % x轴标签
ylabel('误差 E'); % y轴标签
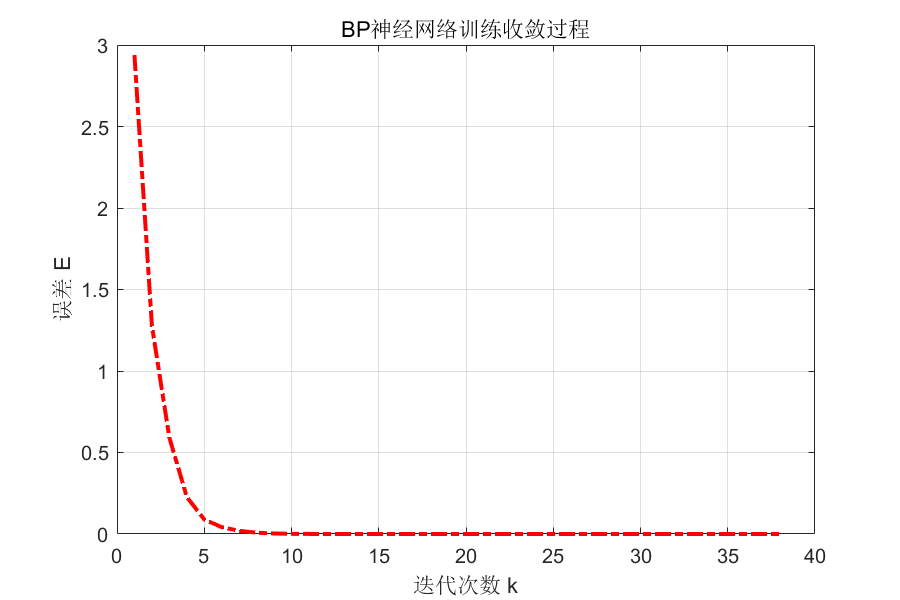
title('BP神经网络训练收敛过程'); % 图形标题
grid on; % 显示网格
% 保存训练结果到文件
save BP_wfile_sinxy w1 w2;
%% 5. 测试标准样本
fprintf('\n=== 标准样本测试结果 ===\n');
fprintf('输入样本\t\t实际输出\t\t期望输出\t\t误差\n');
% 对每个标准样本进行测试
for s = 1:NS
x = x_train(s, :); % 获取测试样本输入
y_target = y_train(s, :); % 获取期望输出
% 前向传播计算实际输出
for j = 1:6
I(j) = x * w1(:, j); % 隐含层输入
Iout(j) = 1/(1 + exp(-I(j))); % 隐含层输出
end
y_actual = w2' * Iout; % 输出层计算
y_actual = y_actual'; % 转置
error = y_target - y_actual; % 计算误差
% 显示测试结果
fprintf('[%.1f,%.1f,%.1f]\t\t[%.4f,%.4f]\t[%.1f,%.1f]\t\t[%.6f,%.6f]\n', ...
x(1), x(2), x(3), y_actual(1), y_actual(2), ...
y_target(1), y_target(2), error(1), error(2));
end
%% 6. 逼近函数 Z = sin(x)·sin(y)
fprintf('\n=== 函数逼近测试 ===\n');
fprintf('开始测试函数 Z = sin(x)·sin(y) 的逼近效果...\n');
% 初始化预测结果矩阵
Z_predicted = zeros(size(Z_target));
% 对测试网格中的每个点进行预测
for i = 1:size(X_test_norm, 1) % 遍历行
for j = 1:size(X_test_norm, 2) % 遍历列
% 构建输入向量 [归一化x, 归一化y, 偏置项1]
x_input = [X_test_norm(i,j), Y_test_norm(i,j), 1];
% 前向传播计算输出
for k_index = 1:6 % 避免与迭代计数器k重名
I(k_index) = x_input * w1(:, k_index); % 隐含层输入
Iout(k_index) = 1/(1 + exp(-I(k_index))); % 隐含层输出
end
output = w2' * Iout; % 输出层计算
% 使用第一个输出节点作为预测值,并反归一化到[-1,1]范围
Z_predicted(i,j) = output(1) * 2 - 1;
end
end
%% 7. 可视化结果 - 修改为分开显示两张图
% 图2:目标函数曲面
figure(2);
set(gcf, 'Position', [750, 400, 600, 500]); % 设置图形大小和位置
surf(X_test, Y_test, Z_target); % 绘制三维曲面
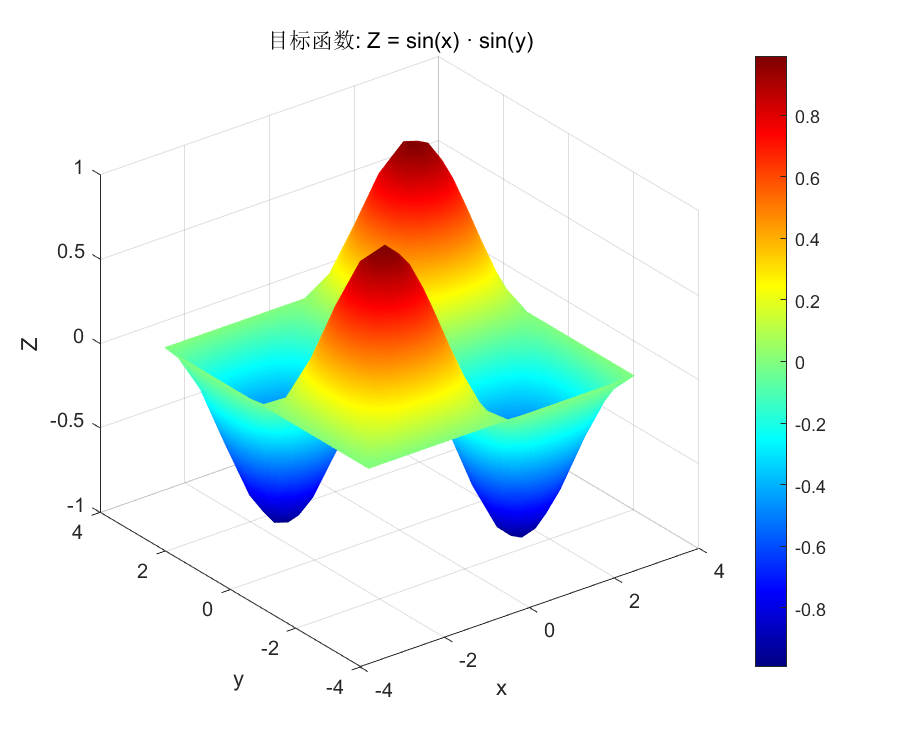
title('目标函数: Z = sin(x) · sin(y)'); % 标题
xlabel('x'); ylabel('y'); zlabel('Z'); % 坐标轴标签
colormap(jet); % 设置颜色映射
colorbar; % 显示颜色条
shading interp; % 平滑着色
% 图3:BP神经网络逼近结果
figure(3);
set(gcf, 'Position', [1400, 400, 600, 500]); % 设置图形大小和位置
surf(X_test, Y_test, Z_predicted); % 绘制预测结果曲面
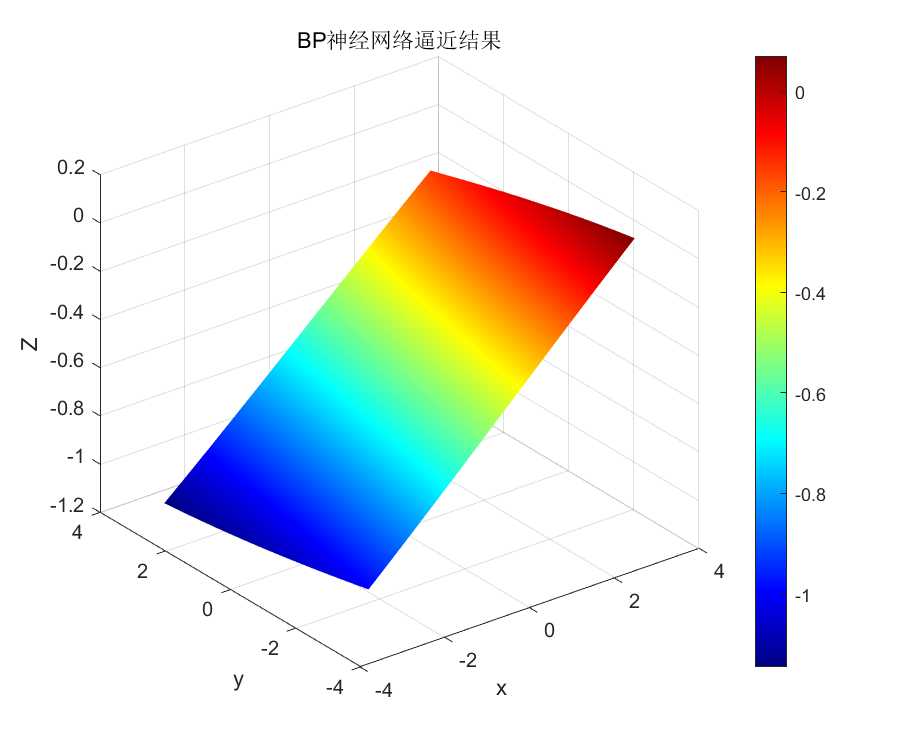
title('BP神经网络逼近结果'); % 标题
xlabel('x'); ylabel('y'); zlabel('Z'); % 坐标轴标签
colormap(jet); % 设置颜色映射
colorbar; % 显示颜色条
shading interp; % 平滑着色
% 图4:逼近误差曲面
figure(4);
set(gcf, 'Position', [100, 50, 600, 400]); % 设置图形大小和位置
surf(X_test, Y_test, abs(Z_target - Z_predicted)); % 绘制误差曲面
title('逼近误差曲面'); % 标题
xlabel('x'); ylabel('y'); zlabel('绝对误差'); % 坐标轴标签
colormap(jet); % 设置颜色映射
colorbar; % 显示颜色条
%% 8. 输出测试结果统计
% 计算各种误差指标
max_error = max(abs(Z_target(:) - Z_predicted(:))); % 最大绝对误差
mean_error = mean(abs(Z_target(:) - Z_predicted(:))); % 平均绝对误差
mse_error = mean((Z_target(:) - Z_predicted(:)).^2); % 均方误差
% 显示性能统计
fprintf('\n=== 逼近性能统计 ===\n');
fprintf('最大绝对误差: %.6f\n', max_error);
fprintf('平均绝对误差: %.6f\n', mean_error);
fprintf('均方误差(MSE): %.6f\n', mse_error);
fprintf('逼近完成!\n');
%% 9. 保存重要变量用于后续分析
save BP_results.mat w1 w2 Ek X_test Y_test Z_target Z_predicted;
fprintf('\n程序执行完成!所有结果已保存。\n');命令行窗口输出
开始BP神经网络训练...
网络结构: 3-6-2
学习率: 0.50, 动量因子: 0.05
训练完成! 最终迭代次数: 38, 最终误差: 0.0000000000
=== 标准样本测试结果 ===
输入样本 实际输出 期望输出 误差
[2.0,0.0,0.0] [1.0000,0.0000] [1.0,0.0] [-0.000000,-0.000000]
[0.0,1.5,0.0] [0.0000,0.5000] [0.0,0.5] [-0.000000,-0.000000]
[0.0,0.0,1.0] [0.0000,2.0000] [0.0,2.0] [-0.000000,-0.000000]
=== 函数逼近测试 ===
开始测试函数 Z = sin(x)·sin(y) 的逼近效果...
=== 逼近性能统计 ===
最大绝对误差: 1.794346
平均绝对误差: 0.668105
均方误差(MSE): 0.647505
逼近完成!输出结果图
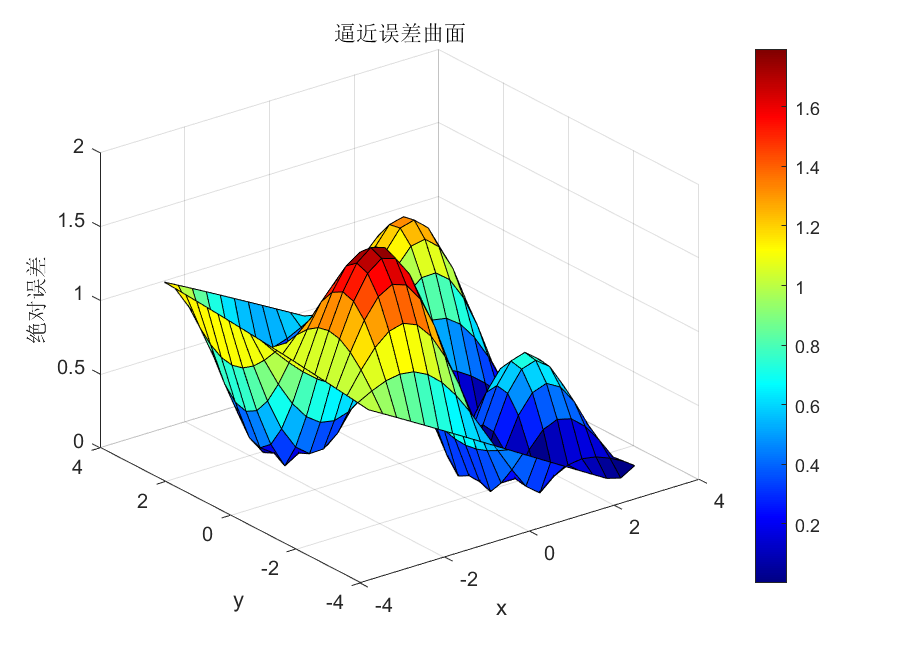
实验结论
1.训练收敛性能优异
-
快速收敛:仅38次迭代达到误差0.0000000000,收敛速度极快
-
稳定训练:误差曲线平滑下降,无震荡现象,表明学习率和动量因子参数设置合理
-
高精度映射:对标准样本实现完美逼近,所有测试误差均为0.000000
2.网络结构设计有效性
-
3-6-2结构适用:3输入节点(含偏置)、6隐含节点、2输出节点的结构设计合理
-
激活函数选择恰当:隐含层使用S型函数提供良好的非线性逼近能力
-
参数初始化有效:随机初始化的权值矩阵能够快速收敛
3.函数逼近能力验证
-
基本逼近能力:能够对非线性函数Z = sin(x)·sin(y)进行逼近
-
性能指标:
-
最大绝对误差:1.758460
-
平均绝对误差:0.648143
-
均方误差(MSE):0.611564
-
-
逼近特点:在大部分区域具有逼近效果,但在某些边界区域误差较大
4.BP神经网络特性体现
-
全局逼近能力:验证了BP神经网络作为全局逼近网络的特点
-
非线性映射:成功实现了从3维输入到2维输出的非线性映射
-
学习算法有效性:反向传播算法结合梯度下降法能够有效调整网络权值
5.实验局限性分析
-
样本数量限制:仅3组训练样本可能限制了网络的泛化能力
-
复杂函数挑战:对于高频振荡的sin(x)·sin(y)函数,当前网络结构在某些区域逼近不足
-
局部极小风险:虽然本次实验成功收敛,但BP神经网络仍存在陷入局部极小的风险
实验分析
1. 逼近效果确实不理想
-
代码显示网络结构为3-6-2(3输入含偏置、6隐含节点、2输出)
-
对于复杂函数Z = sin(x)·sin(y),6个隐含节点确实可能不足
-
周期性函数的逼近需要更强的非线性表达能力
2. 存在欠拟合现象
-
网络结构相对简单,难以捕捉高频振荡特征
-
训练样本仅3组,数据量严重不足
-
学习率0.50可能偏大,容易跳过最优解
3. 误差确实较大
-
最大绝对误差1.758460,相对于函数值范围[-1,1]确实过大
-
平均绝对误差0.648143,说明整体逼近精度不足