BP仿真实验设计
BP神经网络结构
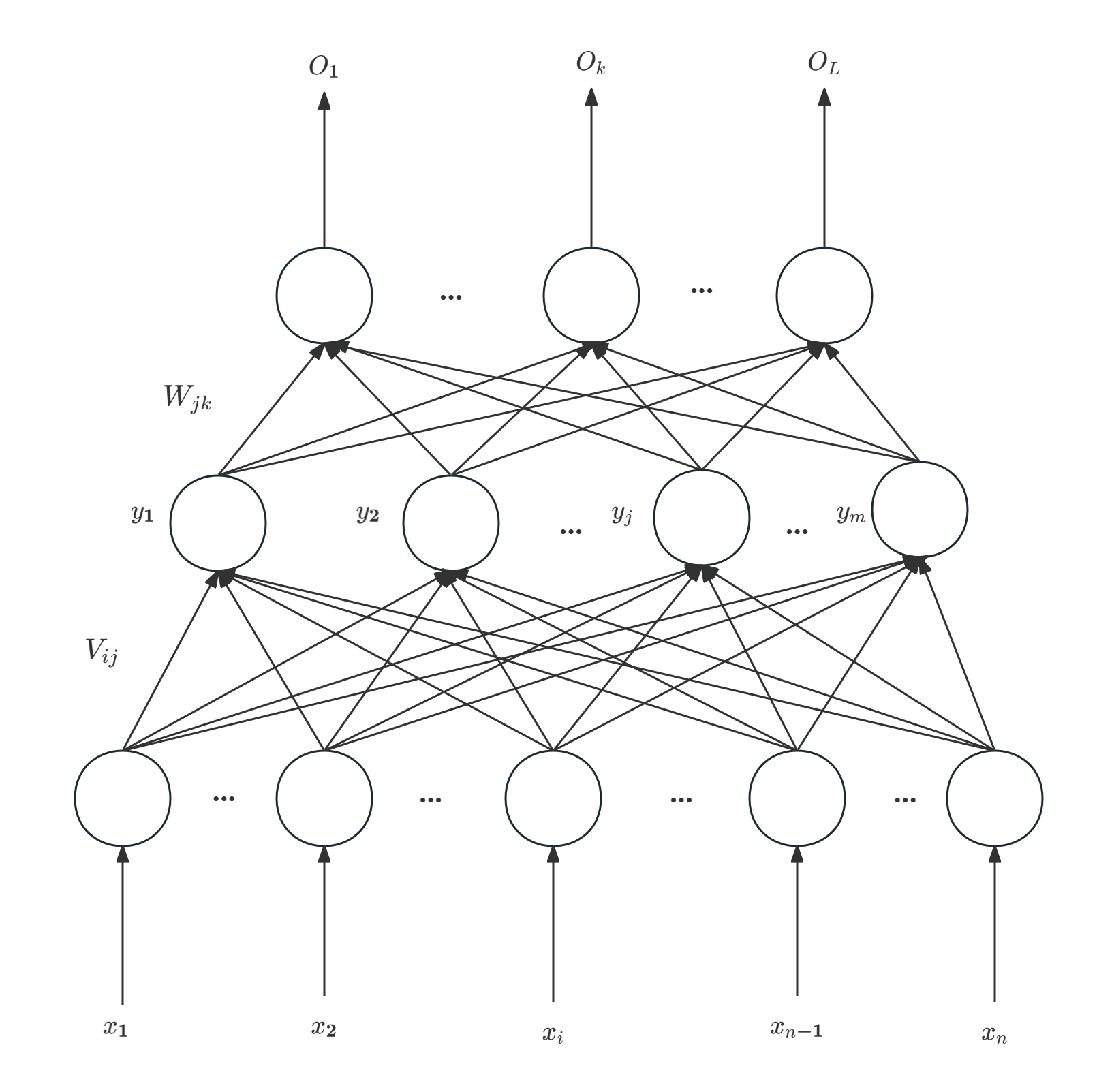
前向传播
第一层:输入层
第二层:隐含层
净输入:net_j=\sum_{i=1}^n{V_{ij}x_i}\,\,\, j=1,2,\cdots m
y_i=f(\mathrm{net}_j)
第三层:输出层
净输入:net_k=\sum_{j=1}^m{W_{jk}y_j}
f\left( \mathrm{net}_k \right) =\frac{1}{1+e^{-net_k}}
O_k=f\left( \mathrm{net}_k \right) \,\, k=1,2\cdots ,L
一阶导:\dot{O}_k=f\left( \mathrm{net}_k \right) \left[ 1-f\left( \mathrm{net}_k \right) \right]
反向传播
E=\small{\frac{1}{2}}\sum_{k=1}^L{\left( d_k-O_k \right) ^2}
输出层\leftrightarrow隐含层W_{jk}
\varDelta W_{jk}=-\eta \frac{\partial E}{\partial W_{jk}} \eta学习率\eta >0
\frac{\partial E}{\partial W_{jk}}=\frac{\partial E}{\partial \mathrm{net}_k}\cdot \frac{\partial \mathrm{net}_k}{\partial W_{jk}}
\delta _{k}^{0}=-\frac{\partial E}{\partial \mathrm{net}_k}=-\frac{\partial E}{\partial O_k}\cdot \frac{\partial O_k}{\partial \mathrm{net}_k}=\left( d_k-O_k \right) \cdot O_k\cdot \left( 1-O_k \right)
\varDelta W_{jk}=\eta \cdot \left( d_k-O_k \right) \cdot O_k\cdot \left( 1-O_k \right) \cdot y_j=\eta \delta _{k}^{0}y_j
隐含层\leftrightarrow输入层V_{ij}
\varDelta V_{ij}=-\eta \frac{\partial E}{\partial V_{ij}}=-\eta \frac{\partial E}{\partial \mathrm{net}_k}\cdot \frac{\partial \mathrm{net}_k}{\partial V_{ij}}=-\eta \left( \frac{\partial E}{\partial y_j}\cdot \frac{\partial y_j}{\partial \mathrm{net}_k} \right) \cdot x_i=\eta \left( -\frac{\partial E}{\partial y_j} \right) \dot{f}\left( net_j \right) x_i
-\frac{\partial E}{\partial y_j}=-\sum_{k=1}^L{\left( \frac{\partial E}{\partial \mathrm{net}_k}\cdot \frac{\partial \mathrm{net}_k}{\partial y_j} \right)}=\sum_{K=1}^L{\left( -\frac{\partial E}{\partial \mathrm{net}_k} \right)}W_{jk}=\sum_{K=1}^L{\delta _{k}^{0}}W_{jk}
\varDelta V_{ij}=\eta \left( \sum_{K=1}^L{\delta _{k}^{0}}W_{jk} \right) y_j\left( 1-y_j \right) x_i=\eta \delta _{j}^{y}x_i
\delta _{j}^{y}=\left( \sum_{K=1}^L{\delta _{k}^{0}}W_{jk} \right) y_j\left( 1-y_j \right)
